Time and Space Complexity

Ok, let's start by telling my laptop configuration, it has 8GB RAM and an i3,10th generation processor. What's yours? There is very less chance that your computer has the same configuration as that mine, we also know that the hardware of computer will decide the runtime of code. In a computer having low hardware specification, it will take more time and with better configuration, it will take less time to run. This means how much time a code will run in someone's else computer is not in hand of the one who is writing code. So what's in our hand? The growth of time taken as the input data increases! Take an example, say my PC take 1 second to evaluate data of 1000 entries and your PC take 0.5 second. Can I control this? A hell No! But let's say on increasing entries from 1000 to 10000, time in my PC increases to 1.5 seconds, Can you give an estimate of time of your PC, if I say it follows a linear relation? Yes! That means absolute time taken is not in our control but time difference for different inputs is controllable. And according to Lord Krishna, we should focus on that thing which is in our control! Also, we have to lower the time taken for large inputs for every machine. This gives rise to time complexity! Let's study it!

Time Complexity

Time complexity is the relation of time with the amount of inputs taken. It's not about time taken! Take an example, say for evaluating 1000 entries time taken is 1 second and for evaluating 2000 entries time taken is 2 seconds then time complexity is neither 1 second nor 2 second and nor difference of these time but time complexity is N! What is N, N is the amount of input! Note that time taken will be different in every machine but this relation that TimeComplexity is related with first power of N will be same in every machine! This is the reason why Time Complexity is very important in the world of programming. A very important point which I want to highlight is that:

While framing the rules for Time Complexity we will use the fact that the amount of Input is very large because that will be the place of concern!

Let's frame the rules:

Constants that are multiplied and added to the expression are ignored!

Reason:

Assume we have data of 10M users and somehow we derived the relation that time complexity is 10N+5. Now according to our point, complexity should be equal to N! Now we don't want actual time but we want to see the growth in time on increasing data. By applying simple mathematics for very large N, 5 can be neglected, more generalized statement is any constant at the place of 5 can be neglected even if it is very large because we can always find a very large number compared to any other number. Now the concern is for 10, for this we should understand what is our need! Is that to calculate actual time? No! we just want to see how time increases. Now t=N and t=10N is telling us same thing that at very large N, t would also be very large or we can say that time grows linearly as N grows! So if I say data is of 10M users that is N=10M, you already know that you should not use that code which follows linear complexity! Now this is independent of the actual expression, no matter whether the actual expression is 10N, 50N or 1000N, they all will tell you the same thing that complexity is linear and a bad choice for very large N! Hence can and should be neglected to keep things simpler!

Less Dominating terms are neglected.

Say if complexity is 𝑁²+𝑁, then complexity will be 𝑁² that means less dominating term 𝑁 is neglected. The reason is very similar to point number 1. As we just want to see how time is growing on increasing 𝑁, so for 𝑁>1, 𝑁ⁿ>.....𝑁³>𝑁²>𝑁. That means only 𝑁ⁿ is enough to tell us that complexity is of order n as rest of the terms will always be less than 𝑁ⁿ so will not give enough information for the choice of code.

Big O notation

Following the above-mentioned two points, we know that Complexity is not the exact relation between time and input but an approximation for checking whether the choice of code is correct or not. So to differentiate complexity from exact relation we use Big O notation, O(Approximated Relation)= time complexity. So O(𝑁) doesn't means t=𝑁, t can be any linear function of 𝑁 but it always be linear, means time will grow linearly! Similarly, O(𝑁²) means time will increase parabolically, actual relation may consist 𝑁 also. This all implies:

O(f(𝑁)) is the upper bound, take an example: O(𝑁³) means the code will always follow the max-to-max cubic relation, it might follow parabolic at some N but can never go for the fourth power of N.

Calculating Time Complexity for any code

For calculating Time complexity keep in mind that we have to consider the worst case as that case is the matter of concern. Now question is: What is worst case? Take an example of Linear Search, worst case is: When element is not in array. Similar with Sorting, when array is oppositely sorted! Let's calculate time complexity of some basic algorithms:

Linear Search

As said above, worst case is when element is not present in array. How many comparisions will it make in that case? N! (Length of array-1), we can also say code has to take N inputs. Hence the time complexity of Linear search is linear or O(𝑁).

Binary Search

Now this is intresting, worst case is same in this case also, when element is not in array. Let's see how many comparisions will it make during this case. Let's say length of array is N. Now mid element will be arr[N/2], first value will be compared. Now as element is not there in array so array length will become N/2 and same process will be repeated. After second comparision, length of array will become N/4. Same will happen after 3,4 and k comparisions; length of array will become $N/8, N/16 $ and $N/2^k$, now note that k will tell us number of comparsions, so O(k) is the time complexity. Now our task is to find k in terms of $N$. Now we know at the end, length of array will become 1. That means at the end,

$N=2^k$

Taking log both sides

$log(N)=k(log(2))$

That implies

$k=log(N)/log(2)$

Hence, complexity is $O(k)=O(log(N)/log(2))=O(log(N))$

Hence binary search follows $log(N)$ complexity.

Bubble Sort

What is the worst case in this code? When array is sorted oppositely. Say if we need increasingly sorted array, but the array is decreasingly sorted. What will happen in this case? Take an example of array; arr=[5,4,3,2,1]. Frstly 5 and 4 will be compared and swapped, hence first comparision is made. SImilarly 5 and 3 will be swapped, then 5 and 2, then 5 and 1. How many comparisions were made total? 4 or we can say arr.length-1 or $N-1$. Now how many comparisions will be there for 4? $N-2$. Similarly for 3,2 and 1 number of comparisions will be $N-3,N-4$ and $N-5$. Note that $N-5=0$. This means total comparsions will be $N-5+N-4+N-3+N-2+N-1$. This also means sum from $0$ to $N$ which is equal to $(N(N-1))/2$. Now applying time complexity rules time complexity will be equal to $O(N^2)$.

These illustrations are enough I think to understand Time Complexity. Now we should move to Mathematical form of Time Complexity.

Mathematical Form Of Time Complexity

As I said $O(g(N))$ is any expression of N. This expression may or may not be equal to $g(N)$, let this expression be $f(N)$. This implies:

$f(N)=O(g(N))$

Now what this $O$ is doing? If you will read the Time Complexity rules carefully then it's just saying this:

$$\lim_{N \to \infty} \frac{f(N)}{g(N)}=a$$

where $a<∞$

Note that this a has no significance, important point is the above inequality.

Now let's assume $f(N)=4N^2+6N+3$, you know that $f(N)$ will give the actual time. Now what is $g(N)$ here? It's $N^2$ or any polynomial of degree 2. Degree can't take any value other than 2. You will see that here any less dominating term or any constant will not affect the inequality $a<∞$. It might affect $a$ but as I said a is useless! Only checking point is this inequality! Hence we neglect less-dominating terms and constant.

Space Complexity

I think enough of time complexity basics are covered. Now let's move to space complexity. After that we will to recursive algorithms. For recursive algorithms, knowledge of space complexity is important, hence we are covering this first!

What is Space Complexity? It's the sum of space given by the problem and extra space which you have used. Take an example, say you are working in an company and they gave you a problem that they will give you an array and you have to return a new sorted array. Now for returning a new array, you have to create it, so you will declare a new array which will use space. So space complexity= Space taken by given array+Space taken by your array. The space taken by your array is called Auxillary Space.

$SpaceComplexity=OriginalSpace+AuxillarySpace$

Recursive Algorithm

Let's analyse the code for writing Fibonacci number using recursion

static int fab(int n){
        if(n<2){
            return n;
        }
      return fab(n-1)+fab(n-2);
    }

Let's debug this for $n=4$

Calling will be from top to bottom and left to right

$fab(3)+fab(2)$, only $fab(3)$ will be in stack, when it will end then $fab(2)$ will move to stack.

$fab(2)+fab(1)$, again $fab(2)$ is in stack

$fab(1)+fab(0)$, $fab(1)$ is in stack, and hence will return 1 and will be finished and hence removed from stack. Now $fab(0)$ will move to stack, return 0 and removed from stack. Outputs will be added and will get to $fab(2)$, which will be finished then and hence removed from stack. Now $fab(1)$ will added to stack, 1 will be returned and then will be removed from stack. Outputs will be added and then move to $fab(3)$ and return the output and hence $fab(3) $ is also now removed from stack. Now $fab(2) $ will be added to stack and similar tree will formed for it, but the height of this tree is less than for that of $fab(3)$. Now if I ask you how many maximum number of functions were there in stack at a time? If you will see carefully, $fab(3),fab(2)$ and $fab(1)$ were there at a time and then$fab(1) $ was removed. Hence maximum number of functions in stack were 3. Now the space taken by these 3 functions is the space taken by your code, because in any other branch of this tree, functions in stack are always less than 3 and hence will take less space. Therefore:

$SpaceComplexity(Recursions)=HeightOfTree$

In this case $HeightOfTree=N$

Hence $SpaceComplexity=O(N)$

Binary Search and Recursion

Normal binary search has constant space complexity as no extra space is taken, even we declare new variables "mid", "start" and "end", still they acquire constant space and constants are ignored in complexities.

Let's take an example of Recursion by writing binary search code using recursions.

 static int srch(int[] arr, int target, int s, int e){
        int mid=(s+e)/2;
        if(s>e){
            return -1;
        }
        if(arr[mid]==target){
            return mid;
        }
        if(arr[mid]<target){
            return srch(arr,target,mid+1, e);
        }

        return srch(arr,target,s,mid-1);
    }

Now calculating time complexity is tough in this case. What we know is, this funcional equation:

$f(N)=f(N/2)+O(1)$

Many questions will be revolving around your head, What is f? What is N? $f(N)$ is the mathematical form of $srch(....)$ function, hence no requirement of array, and $N$ is a difference of e and s ($N$ is size of array in which searching algorithm will move). The last $O(1)$ shows the last comparision which will be made when element will be found. These equations are known as Recursive Relations. In most of the cases it will be easier to find these equations, hence we should find a way to find Time Complexity using these Relations. To do this we have Akkra-Bazi Theorem and some other methods. But before that, we should learn type of recursions.

Divide and Conquer Recursions

Any recursion whose recursive relation is of the form:

$T(N)=a_1T(b_1N+f(N))+a_2T(b_2N+f(N))+.......+a_kT(b_kN+f(N))+g(N)$

Note for Binary Search, $a_1=1,b_1=1/2$ and $g(N)=c$, $c$ is any constant. So Binary Search is a type of Divide and Conquer Recursion. To find complexity of these recursions, we use Akkra-Bazi Theorem.

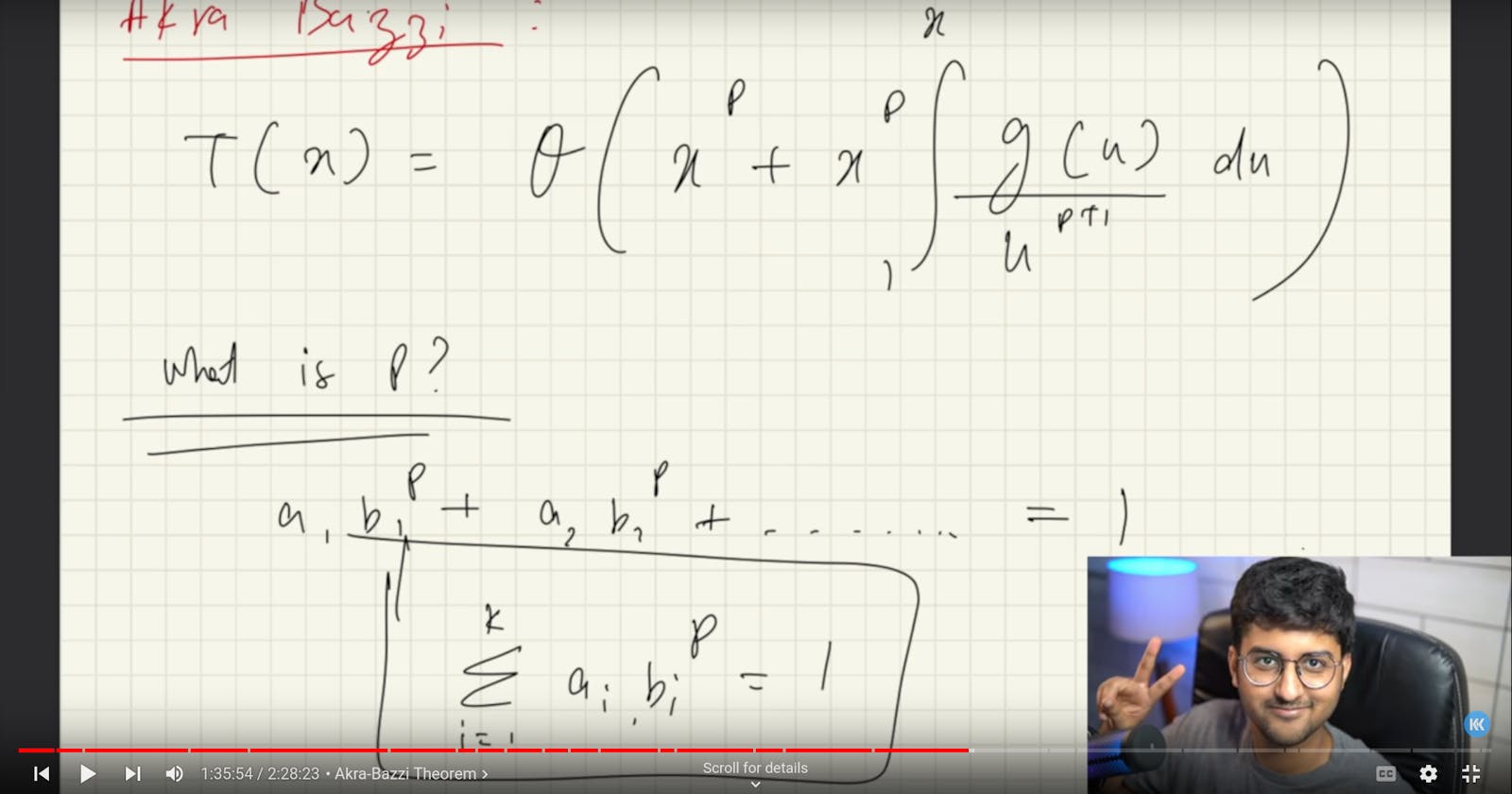
Akkra-Bazi Theorem

Akkra-Bazi Theorem Says, if time complexity is $T(N)$, then

$T(N)=O(N^p+N^p\int_{1}^{N}\frac{g(u)}{u^{p+1}}du)$

where $p$ is a real number satisfying:

$$\sum_{i=1}^{k}a_ib_i^p=1$$

Example: Binary Search

$f(N)=f(N/2)+O(1)$

$a_1=1,b_1=1/2$

$g(N)=c$

$k=1$

$a_1*b_1^p=1$

$1*\frac{1}{2}^p=1$

This implies

$p=0$

Putting $p$ in the equation

$T(N)=O(clog(N))=O(logN)$

Case when $p$ can't be found

Take an example:

$T(N)=3T(N/3)+4T(N/4)+N^2$

By hit and trial you can see that 1 is not coming. Like when $p=1$

$$\sum=2$$

I have used $\sum$ to denote that summation. I hope you will understand!

When $p=2$

$$\sum=\frac{7}{12}<1$$

This means \(1

You can use logarithms but it will make the problem messy. Let's do it in another way!

We know,

$g(N)=N^2$

This means

$\frac{g(u)}{u^{p+1}}=u^{1-p}$

Now integrating it and applying the formula

$T(N)=O(N^p+N^p*(\frac{N^{2-p}}{2-p}-\frac{1}{2-p}))$

$p<2$, hence by neglecting less dominating terms, that is $N^p$,

$T(N)=O(N^2)$

This means when \(p

Linear Recursions

Any recursion, following a recursive relation of the form:

$f(N)=\sum_{i=1}^{n}a_if(N-i)$

Now again our aim is to calculate Time-Complexity of this recursion using this relation.

Method-1

Put $f(N-i)=\alpha^{N-i}$

Now equation becomes

$\alpha^N=\sum_{i=1}^{n}a_i\alpha^{N-i}$

Again by applying simple algebra, this equation becomes:

$\alpha^n-a_1\alpha^{n-1}-a_2\alpha^{n-2}-......-a_n=0$

Let the roots of this equation be $\alpha_1,\alpha_2,.......,\alpha_n$

As $\alpha$ is the assumed function so it can be written as:

$f(N)=c_1\alpha_1^N+c_2\alpha_2^N+.......+c_n\alpha_n^N$

Proof of this is out of the scope of this "Coding Blog"

Now to find n constants we should have n equations and these n equations are the base value of recursions, like 0 and 1 in Fibonacci number.

If we know $f$ in the form of roots, then $O(f(N))$ will give the time complexity of the code and even recursive relation can be replaced by $O(f(N))$. One can try this approach for Fibonacci number recursive relation.

This was the case of distinct roots, if a root $\alpha_1$ is repeated r times and rest of the roots are distinct, then

$f(N)=(c_1+c_2N+.....+c_rN^{r-1})\alpha_1^N+c_{r+1}\alpha_2^N+......+c_n\alpha^N$

Proof of this can be found easily in some differential equation books.

Non-Homogenous Linear Recursions

Any recursion, following a recursive relation of the form:

$f(N)=(\sum_{i=1}^{n}a_if(N-i))+g(N)$

Now, those who have studied ODE in their College can easily connect. Firstly we have to find the solutions of Homogenous Equation that is ignore $g(N)$, then find the particular solution $\alpha_p$ and $f(N)$ will be

$f(N)=c_1\alpha_1^N+c_2\alpha_2^N+.......+c_n\alpha_n^N+\alpha_p$

In order to get particular solution, we assume P.S and then put in the original equation (very first equation of this section) and then compare the coefficients. This method is called Method of Undetermined Coefficients. The ways to assume P.S is:

If $g(N)=A\alpha^N$, then we assume $\alpha_p=B\alpha^N$
if $g(N)=P_n$ where $P_n$is the polynomial of degree $n$ then assume in variable N, then assume $\alpha_p=A_0+A_1N+....+A_nN^n$
If $g(N)$ is logarithmic function or any other then Variation of Parameter Method is used, which can be learnt through Books and YouTube.

i think, this is enough for Time and Space Complexity basics. So that's it from my side. I hope you liked it!